Dnes lze slovo „integrální“ slyšet poměrně často a často i na nejneočekávanějších místech, například na burzovním kanálu v televizi nebo v novinách. Často slyšíme výraz "integrální indikátory", slovo "integrovaný", "integrativní" a podobně. Celkově jsou úředníci a televizní moderátoři obecně velmi rádi různým slovům, i když je nepravděpodobné, že pochopí jejich pravý význam. A dnes budeme hovořit o tom, co je integrál, jaké typy integrálu existují a jaké jsou jejich rozdíly.
Co je integrál
Integrál je latinské slovo, které k nám přišlo ze starověku a znamená „Celé“ nebo „Plné“. To je, to je jasné, že jestliže objekt byl řeknut o objektu, například, nádoba mléka, to znamenalo, že to bylo plné, a tam bylo tolik mléka v tom jak to bylo.
Časem se toto slovo začalo používat ve zcela odlišných disciplínách - ve filosofii, politice, ekonomii, v algebře a geometrii. Nejjednodušší výklad integrálu je však dán matematikou.
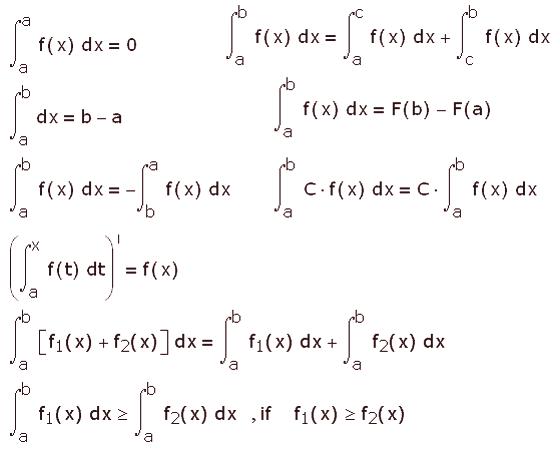
Určitý integrál
Integrál je tedy určitý součet jednotlivých částí. Zde jsou nejjednodušší příklady jasnějšího pochopení podstaty tohoto výrazu:
- Předmětem je integrál (součet) molekul.
- List v buňce je integrální (součet) buněk.
- Sluneční soustava je integrál (součet) Slunce a planet.
- Společnost je integrál lidí.
- Segment je integrál (součet) metrů. Je-li malý segment, pak centimetry, milimetry nebo mikroskopické segmenty.
- OblastJakýkoliv povrch je integrál čtverečních metrů, čtverečních centimetrů nebo milimetrů a také mikroskopických oblastí.
- Objem je integrál kubických metrů nebo, jak se také nazývá, litry.
Co jsou definovány a neurčité integrály?
Začněme s určitým, protože jeho význam je lépe pochopitelný.
Geometrie studuje oblasti . Například, pokud chcete lepidlo tapety doma, musíte znát oblast stěn zjistit, kolik tapet byste měli koupit. Pak jednoduše vynásobíte délku stěny výškou a získáte její plochu. V tomto případě je tato oblast integrálem čtverečních metrů nebo centimetrů, v závislosti na jednotkách, ve kterých jste měřili. Povrchy, jejichž plochu potřebujeme vypočítat, však nemají vždy tvar obdélníku, čtverce nebo dokonce kruhu. Ve většině případů se jedná o složité tvary s vlnitými stranami. Nejběžnějším příkladem je plocha obrázku pod křivkou, která má rovnici y = 1 /x. Faktem je, že je nemožné najít jeho oblast pomocí obyčejných vzorců, podle kterých nacházíme oblast čtverce, kruhu nebo dokonce koule. Pro tento účel byl vyvinut určitý integrál.
Podstatou metody je, že naše složitá postava musí být rozdělena na velmi úzké obdélníky, tak úzké, že výška každé ze dvou sousedních je téměř stejná. Je zřejmé, že ve skutečnosti je možné zmenšit tloušťku těchto obdélníků nekonečně, takže velikost dx se používá k označení jejich tloušťky. X je souřadnice a předpona d jeoznačení nekonečně klesající hodnoty. Když tedy píšeme dx - to znamená, že vezmeme segment podél osy x, jehož délka je velmi malá, téměř nulová.
Již jsme se tedy shodli na tom, že plocha jakéhokoli čísla je integrálem čtverečních metrů nebo jakýchkoli jiných postav s menšími plochami. Pak je naše postava, jejíž oblast hledáme, integrál nebo součet těch nekonečně tenkých obdélníků, do kterých jsme jej rozdělili. A jeho plocha je součtem jejich oblastí. To znamená, že naším celým úkolem je najít oblast každého z těchto obdélníků a pak je všechny přidat - to je určitý integrál.
Teď pojďme mluvit o neurčitém integrálu. Abychom pochopili, co to je, musíte se nejprve dozvědět o derivaci. Začněme.
Derivace je úhel sklonu tečny k nějakému grafu v určitém bodě. Jinými slovy, derivace je nakolik je graf nakloněn na daném místě. Například přímka v libovolném bodě má stejný sklon a křivka je odlišná, ale lze ji opakovat. Pro výpočet derivace existují speciální vzorce a proces jejich výpočtu se nazývá diferenciace. Tj diferenciace je stanovení úhlu grafu v daném bodě.

Tabulka základních neurčitých integrálů
A aby bylo možné postupovat opačně - zjistit vzorec grafu jeho úhlem sklonu, uchylují se k operaci integrace nebo k součtu údajů o všech bodech. Integrace a diferenciacedvou vzájemných procesů. Pouze zde nepoužívají integrál, který byl v prvním odstavci (pro určení oblasti), ale druhý - neurčitý, tj. Bez omezení.
Předpokládejme, že víme, že derivace určité funkce je rovna 5. 5 je úhel sklonu grafu k ose x v daném bodě. Poté, když integrujeme derivaci, zjistíme, že funkce tohoto derivátu, který se také nazývá primitivní, je y = 5x + c, kde c je libovolné číslo. Pro integraci i pro diferenciaci existují speciální vzorce, které lze nalézt v tabulkách.
Závěr
Na závěr shrneme, že hlavní rozdíl mezi určitým integrálem a neurčitým je v jejich úkolech. Určité integrály se používají k výpočtu omezených parametrů, jako je plocha, délka nebo objem, a neurčitý, když se vypočítávají parametry, které nemají žádné hranice, tj. Funkce.
Zajímavé video na toto téma: